Two Angles That Form A Linear Pair
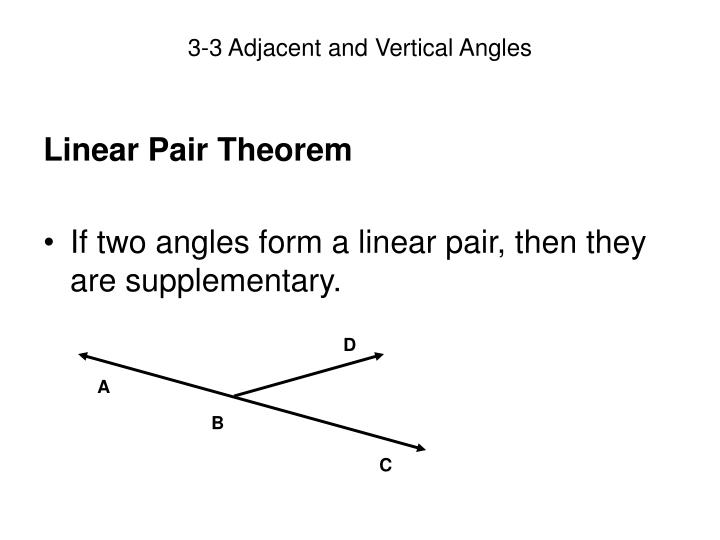
Two Angles That Form A Linear Pair - In the figure, ∠ 1 and ∠ 2 form a linear pair. This fact leads to a wide range of properties and applications. Web the two angles make a linear pair, so the sum of measures of the two angles is 180°\text{\textdegree}°. The sum of two angles in the linear pair is always 180 degrees. The steps to using this postulate are very. Linear pairs of angles are also referred to as supplementary. Web up to 6% cash back a linear pair is a pair of adjacent angles formed when two lines intersect. Web not all supplementary angle form a linear pair. Two angles are said to form a linear pair if they add up to 180 degrees. Web however, just because two angles are supplementary does not mean they form a linear pair.
The steps to using this postulate are very. Web the two angles make a linear pair, so the sum of measures of the two angles is 180°\text{\textdegree}°. Web the linear pair postulate says if two angles form a linear pair, then the measures of the angles add up to 180°. Web there are some properties of linear pair of angles and they are listed below: It should be noted that all linear pairs are supplementary because. In the figure, ∠ 1 and ∠ 2 are supplementary by the. The sum of two angles in the linear pair is always 180 degrees. Supplementary angles are two angles whose same is 180^o linear. This fact leads to a wide range of properties and applications. Web up to 6% cash back the supplement postulate states that if two angles form a linear pair , then they are supplementary.
(a) 50 ° + 40 ° = 90 °. So that means <1 + <2 =180 but let’s call those. Supplementary angles are two angles whose same is 180^o linear. A linear pair are two angles that makes a line. Web however, just because two angles are supplementary does not mean they form a linear pair. Web up to 6% cash back the supplement postulate states that if two angles form a linear pair , then they are supplementary. We now have an equation in two unknowns. Two angles are said to form a linear pair if they add up to 180 degrees. Web the two angles make a linear pair, so the sum of measures of the two angles is 180°\text{\textdegree}°. So do ∠ 2 and ∠ 3 , ∠ 3 and ∠ 4 , and.
Linear pair
Web first we need to define what is a linear pair? In the figure, ∠ 1 and ∠ 2 are supplementary by the. The steps to using this postulate are very. In the diagram below, ∠abc and ∠dbe are supplementary since 30°+150°=180°,. Since the sum of angles is not equal to 90 °, the angles 50 ° and 40 °.
Definition and Examples of Linear Pairs YouTube
The sum of linear pairs is 180°. Web there are some properties of linear pair of angles and they are listed below: The sum of two angles in the linear pair is always 180 degrees. If the two angles form a linear pair, then the sum of the two angles equals 180 degrees. In the figure, ∠ 1 and ∠.
PPT 33 Adjacent and Vertical Angles PowerPoint Presentation ID6953038
In the figure, ∠ 1 and ∠ 2 form a linear pair. Web there are some properties of linear pair of angles and they are listed below: Web the linear pair postulate says if two angles form a linear pair, then the measures of the angles add up to 180°. In the diagram below, ∠abc and ∠dbe are supplementary since.
Linear Pair lines and angles This postulate is sometimes call the
This fact leads to a wide range of properties and applications. Since the sum of angles is not equal to 90 °, the angles 50 ° and 40 ° do. Web when two lines intersect each other, the adjacent angles make a linear pair. In the figure, ∠ 1 and ∠ 2 form a linear pair. Web the linear pair.
Which statement is true about this argument? Premises If two angles
Web however, just because two angles are supplementary does not mean they form a linear pair. In the figure, ∠ 1 and ∠ 2 form a linear pair. It should be noted that all linear pairs are supplementary because. So do ∠ 2 and ∠ 3 , ∠ 3 and ∠ 4 , and. Supplementary angles are two angles whose.
Two angles form a linear pair. The measure of one CameraMath
Supplementary angles are two angles whose same is 180^o linear. Web first we need to define what is a linear pair? We now have an equation in two unknowns. Web the linear pair postulate says if two angles form a linear pair, then the measures of the angles add up to 180°. Two angles are said to form a linear.
📈In which diagram do angles 1 and 2 form a linear pair?
Linear pairs of angles are also referred to as supplementary. A linear pair are two angles that makes a line. The sum of linear pairs is 180°. Web when two lines intersect each other, the adjacent angles make a linear pair. So that means <1 + <2 =180 but let’s call those.
PPT Geometry Review Angles and Parallel Lines PowerPoint Presentation
Web the two angles make a linear pair, so the sum of measures of the two angles is 180°\text{\textdegree}°. The sum of linear pairs is 180°. So do ∠ 2 and ∠ 3 , ∠ 3 and ∠ 4 , and. This fact leads to a wide range of properties and applications. A line is 180 degrees.
The two angles below form a linear pair, and the expressions are
(a) 50 ° + 40 ° = 90 °. So do ∠ 2 and ∠ 3 , ∠ 3 and ∠ 4 , and. In the diagram below, ∠abc and ∠dbe are supplementary since 30°+150°=180°,. Web when two lines intersect each other, the adjacent angles make a linear pair. Linear pairs of angles are also referred to as supplementary.
Name two angles that form a linear pair.
Supplementary angles are two angles whose same is 180^o linear. In the given diagram, o a and o b are. We now have an equation in two unknowns. Web when two lines intersect each other, the adjacent angles make a linear pair. Web the two angles make a linear pair, so the sum of measures of the two angles is.
We Now Have An Equation In Two Unknowns.
The sum of two angles in the linear pair is always 180 degrees. Web not all supplementary angle form a linear pair. A linear pair are two angles that makes a line. If the two angles form a linear pair, then the sum of the two angles equals 180 degrees.
Web Linear Pair Of Angles Are Two Angles That Form A Straight Angle (Angle Measuring 180 Degrees).
So that means <1 + <2 =180 but let’s call those. Two angles are said to form a linear pair if they add up to 180 degrees. Web first we need to define what is a linear pair? Web up to 6% cash back the supplement postulate states that if two angles form a linear pair , then they are supplementary.
Since The Sum Of Angles Is Not Equal To 90 °, The Angles 50 ° And 40 ° Do.
A line is 180 degrees. The steps to using this postulate are very. This fact leads to a wide range of properties and applications. Web up to 6% cash back a linear pair is a pair of adjacent angles formed when two lines intersect.
In The Figure, ∠ 1 And ∠ 2 Form A Linear Pair.
Web when two lines intersect each other, the adjacent angles make a linear pair. Web however, just because two angles are supplementary does not mean they form a linear pair. The sum of linear pairs is 180°. Web the two angles make a linear pair, so the sum of measures of the two angles is 180°\text{\textdegree}°.